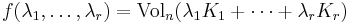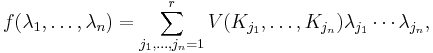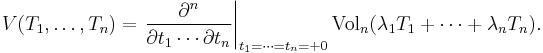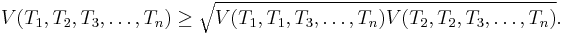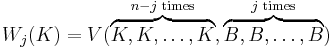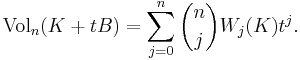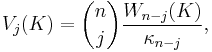Mixed volume

In mathematics, more specifically, in convex geometry, the mixed volume is a way to associate a non-negative number to an n-tuple of convex bodies in the n-dimensional space. This number depends on the size of the bodies and their relative positions.^[1]

Contents 1 Definition 2 Properties 3 Quermassintegrals 3.1 Intrinsic volumes 3.2 Hadwiger's characterization theorem 4 Notes

Definition

Let K₁, K₂, ..., K_r be convex bodies in Rⁿ, and consider the function

of non-negative λ-s, where Vol_n stands for the n-dimensional volume. One can show that f is a homogeneous polynomial of degree n, therefore it can be written as

where the functions V are symmetric. Then V(T₁, ..., T_n) is called the mixed volume of T₁, T₂, ..., T_n.

Equivalently,

Properties

• The mixed volume is uniquely determined by the following three properties:

1. V(T, ...., T) = Vol_n(T);
2. V is symmetric in its arguments;
3. V is multilinear: V(a T + b S, T₂, ..., T_n) =a V(T, T₂, ..., T_n) + b V(S, T₂, ..., T_n) for a,b ≥ 0.

• The mixed volume is non-negative, and increasing in each variable.

• The Alexandrov–Fenchel inequality, discovered by Aleksandr Danilovich Aleksandrov and Werner Fenchel:

Numerous geometric inequalities, such as the Brunn–Minkowski inequality for convex bodies and Minkowski's first inequality, are special cases of the Alexandrov–Fenchel inequality.

Quermassintegrals

Let K ⊂ Rⁿ be a convex body, and let B ⊂ Rⁿ be the Euclidean ball. The mixed volume

is called the j-th quermassintegral of K.^[2]

The definition of mixed volume yields the Steiner formula (named after Jakob Steiner):

Intrinsic volumes

The j-th intrinsic volume of K is defined by

where κ_n−j is the volume of the (n − j)-dimensional ball.

Hadwiger's characterization theorem

Hadwiger's theorem asserts that every valuation (measure theory) on convex bodies in Rⁿ that is continuous and invariant under rigid motions of Rⁿ is a linear combination of the quermassintegrals (or, equivalently, of the intrinsic volumes).^[3]

Notes